Pythonを使って、粒子の画像データから粒子層の厚みを評価するコードを作成しました。
ここでは以下のように楕円(=黒い粒子)が分散している仮想的に作成した画像から、粒子が分散している層の厚み(上下方向)を評価します。また、長さの単位はpixelとしています。

検討案
以下4つの方法を検討します。
①縦方向に、楕円の上端と下端の長さを評価する(下図、2本の赤線間の長さ)

②小さい領域を削除した後、①の評価

③最大の連続領域を取得して、①の評価

④opening処理で近い領域を結合させた後、最大の連続領域を取得して、①の評価

コード
まず画像を読み込みます。
import cv2
import matplotlib.pyplot as plt
import numpy as np
from skimage import morphology
from skimage.measure import label
from skimage.morphology import disk, opening
# pathを設定
path = './pic/sample_gray.png'
# モノクロ画像として読み込み
img_gray = cv2.imread(path,cv2.IMREAD_GRAYSCALE)
img_gray = img_gray==255
# 型を確認
print(f'type: {type(img_gray)}')
# 次元を確認
print(f'shape: {img_gray.shape}')
# 読み込んだ画像を表示
plt.imshow(img_gray,cmap=plt.cm.gray)
plt.show()
①~④の処理は以下のようなメソッドを作成しました。
# 1の処理
def calc_length(img_gray):
upper_list=[]
lower_list=[]
length_list=[]
for i in range(img_gray.shape[1]):
particle_index = np.where(img_gray[:,i]==False)[0]
upper_list.append(particle_index.min())
lower_list.append(particle_index.max())
length_list.append(particle_index.max() - particle_index.min())
return upper_list,lower_list,length_list
# 2の処理
def process_2(img_gray, th=10000):
return morphology.remove_small_holes(img_gray, area_threshold=th)
# 3の処理
def process_3(img_gray):
label_image=label(img_gray==False, connectivity=1)
max_label=1
max_area=0
for i in range(1,label_image.max()+1):
area=(label_image==i).sum()
if max_area<area:
max_label=i
max_area=area
return label_image!=max_label
# 4の処理
def process_4(img_gray,radius=20):
footprint = disk(radius=radius)
opened = opening(img_gray, footprint)
return opened
# 結果の出力
def plot_result(upper, lower, length):
print(f'mean:\t{np.mean(length):.1f}')
print(f'median:\t{np.median(length):.1f}')
print(f'std:\t{np.std(length):.1f}')
plt.imshow(img_gray,cmap=plt.cm.gray)
plt.plot(range(img_gray.shape[1]),upper,c='red', lw=4)
plt.plot(range(img_gray.shape[1]),lower,c='red', lw=4)
plt.show()
plt.hist(length)
plt.ylabel('num')
plt.xlabel('length')
plt.show()結果
処理を実行します。
# 検討案1
upper_1, lower_1, length_1=calc_length(img_gray)
print('検討案1')
plot_result(upper_1, lower_1, length_1)
# 検討案2
img_2 = process_2(img_gray)
upper_2, lower_2, length_2=calc_length(img_2)
print('検討案2')
plot_result(upper_2, lower_2, length_2)
# 検討案3
img_3 = process_3(img_gray)
upper_3, lower_3, length_3=calc_length(img_3)
print('検討案3')
plot_result(upper_3, lower_3, length_3)
# 検討案4
img_4_tmp = process_4(img_gray)
img_4 = process_3(img_4_tmp)
upper_4, lower_4, length_4=calc_length(img_4)
print('検討案4')
plot_result(upper_4, lower_4, length_4)検討案①
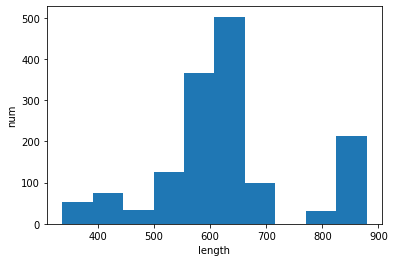
mean: 624.0, median: 618.0, std: 120.0

検討案②
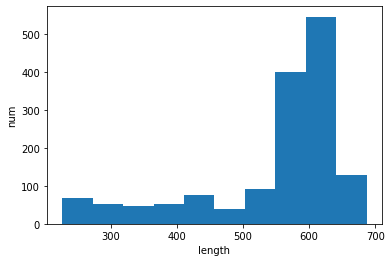
mean: 547.0, median: 589.0, std: 112.2

検討案③
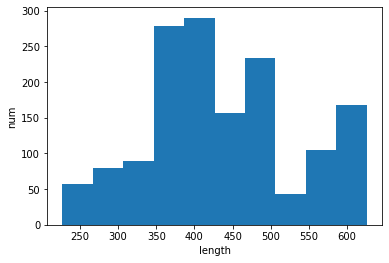
mean: 434.9, median: 421.0, std: 98.5

検討案④
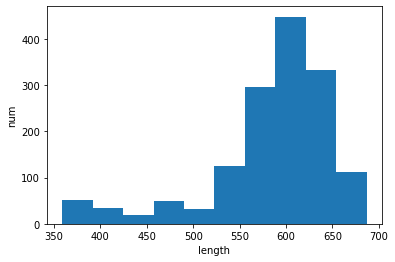
mean: 583.7, median: 599.0, std: 68.0

比較
検討案①は、粒子がいる領域を全て評価しているので、下側に大きく離れた2粒子も含まれており層の厚みとしては過大評価されている印象があります。
検討案②では、①であった過大評価を回避できていますが、一方で層に含まれても良さそうな独立した粒子が無視されており、層の厚みとしては過小評価されています。
検討案③では、②に比べてより過小評価されていることがうかがえます。
検討案④では、パラメータで設定した距離以下で離れている粒子を同一の領域として扱っているので、①②③で見られた評価の偏りが改善されていることが分かります。
まとめ
Pythonを使って、粒子の画像データから粒子層の厚みを評価するコードを作成しました。検討案④の方法が層の厚みとして妥当そうな評価をしていますが、場面によって求められる評価方法は変わってくるので、ニーズに合わせてこれらの方法から選ぶことが良いと思います。
今回作成したプログラムを、streamlitでwebアプリ化しました。


コメント