画像処理エンジニア検定の勉強中に出てきた単語のまとめです。
こちらの本を参考にしています。
https://amzn.to/3TLLjQt
| 単語 | 内容 |
|---|---|
| 標本化・量子化 | アナログ信号から離散的な位置におけるアナログ値を取り出す処理を標本化(sampling)とよぶ。画像の標本化では、2次元的な像(アナログ画像)の光強度に対して、縦横に等間隔の格子状に配置した標本点における光強度を電圧値として取り出す。この標本点の間隔を、標本化間隔とよび、標本点におけるアナログ値を標本値とよぶ。 標本値を有限分解能の数値に変換する処理を、量子化(quantization)とよぶ。量子化では、連続値を量子化レベル数個の離散値に置き換えるため、丸め誤差が生じる。この誤差を量子化誤差とよぶ。アナログ画像の値の範囲が同じときには、量子化レベル数が大きいほど量子化誤差は小さくなる。一般的には8ビット量子化した画像を利用することが多い。 |
| 標本化定理 | アナログ信号が\(f_{max}\)に帯域制限されているとき、\(2f_{max}\)以上の標本化周波数で評価すればアナログ信号の情報を失わない。 |
| エイリアシング | 信号が標本化され再生されたとき、元の信号とエイリアスとが重なって生じる歪みのこと。 空間周波数が高いために生じるので、縮小処理の前にローパスフィルタで最高空間周波数を低くすることで低減できる。 |
| 回転行列 | 3次元空間上の点\((X, Y, Z)\)を、\(Z\)軸周りに角度\(\theta\)だけ回転させる回転行列は、変換後の座標を\((X’,Y’,Z’)\)として以下のように表される。ここで回転の方向は、\(x\)軸を\(y\)軸に向ける方向である。 \(\left( \begin{matrix} X’ \\ Y’ \\ Z’ \end{matrix} \right) = \left( \begin{matrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right) \left( \begin{matrix} X \\ Y \\ Z \end{matrix} \right)\) |
| プレヴィットフィルタ | エッジフィルタの1種で、横方向、縦方向でそれぞれ微分を取り、両方の結果を合成するフィルタである。隣と比べて明るさが変化している箇所を強調する。 横方向 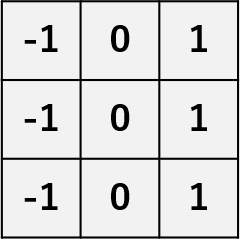 縦方向 縦方向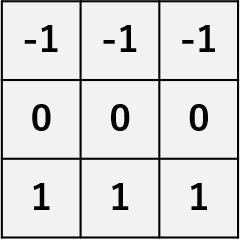 |
| ソーベルフィルタ | エッジフィルタの1種でプレヴィットフィルタ同様、横方向、縦方向でそれぞれ微分を取り、両方の結果を合成するフィルタである。中央部の画素に重みづけを行い、中央部がより強調される処理を行う。 プレヴィットフィルタと比べ、輝度差が少ないエッジも強調できますが、ノイズも強調されてしまう傾向がある。 横方向 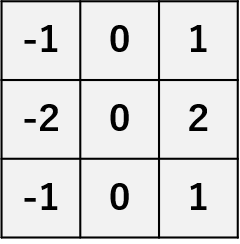 縦方向 縦方向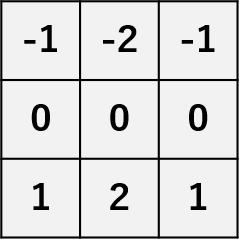 |
| ラプラシアンフィルタ | プレヴィットフィルタとソーベルフィルタ、ロバーツフィルタは1次微分フィルタと呼ばれるもので、1階微分を行う。対して、ラプラシアンフィルタは2階微分を行う2次微分フィルタに対応する。 1次微分では隣り合った画像の明るさの差が大きいところが強調されるため、光が当たっている箇所と影になっている箇所の境目 などの輪郭ではないが隣との差がある箇所も強調される。そのような場合に2次微分を使うと、微分を2回行うため差分量の変化が大きいところのみを強調することができる。なお、微分を繰り返すためエッジだけでなくノイズを強調してしまう可能性があり、メディアンフィルタやガウシアンフィルタを適用し、平滑化を行ってからラプラシアンフィルタの処理をかけることが多い。 4近傍 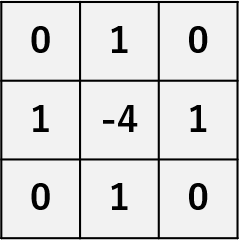 8近傍 8近傍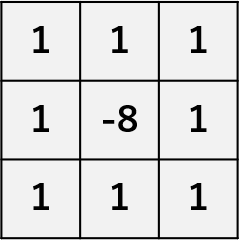 |
| シェーディング補正 | レンズの収差、照明ムラ等を補正する方法。レンズを用いて撮像する場合に、中央部に比べ周辺部が暗くなる現象が起こり、この差は、絞りを開放にするほど大きくなる。シェーディング補正の手法には多くの方法がありますが、基本的には全体的な明暗の変化を表した明暗分布画像で元の画像を除算して、全体の明るさの補正を行う。 |
| アダブースト | 基本的には、2値分類の機械学習モデル。ブースティングモデルの一種で、弱学習機を逐次的に生成していくアルゴリズム。大きく分けて以下の四つの特徴がある。 ・弱学習機の訓練において、重み付けられたデータ集合を利用する ・前の学習機が誤分類したデータ点に大きな重みを与える ・最初は全てのデータに均等な重みを与える ・そのように生成・訓練した弱学習機を組み合わせて最終的な予測値を出力する このように、AdaBoostは誤分類したデータを重要視することによって制度を高めようとするアルゴリズムであるといえる。 |
| 双方向反射率分布関数 (BRDF) | ある点\(x_i\)にある方向\(\boldsymbol{\omega_i}\)から入射した光が別の点\(x_o\)から別の方向\(\boldsymbol{\omega_o}\)に向かって出射することを考える。このとき、\(x_i\)に入射する放射束を\( d\Phi_i(x_i, \boldsymbol{\omega_i}) \)、その放射束によって\(x_o\) から反射する放射輝度を\( dL_r(x_o, \boldsymbol{\omega_o}) \)で表す。一般的には\( dL_r\)は\(d\Phi_i\)に比例し、次に示すような関係を持つ。 \[ d L_r = S d\Phi_i \] この比例係数\(S\)は一般的には入射光の物体表面上の位置と入射方向、出射光の位置と入射方向に依存して変化する関数であるため次のように表される。 \[ S = S(x_i, \boldsymbol{\omega_i}, x_o, \boldsymbol{\omega_o}) \] ここで入射光と出射光の間の距離がゼロ、光は入射したところから反射していくという近似を考えれば、ある点\(x\)の出射光に寄与するのは同じ点に入射した放射束のみとなる。そのような局所的な領域における入射光と出射光の関係は微小放射束\(d\Phi_i\)の代わりに微小放射照度\( dE_i(x, \boldsymbol{\omega_i}) \)を使って表すことができる。そしてある点\(x\)を出射する放射輝度\( dL_r(x, \boldsymbol{\omega_o}) \)と次のように関係付けることができる。 \[ d L_r(x, \boldsymbol{\omega_o}) = f_r(x, \boldsymbol{\omega_i}, \boldsymbol{\omega_o}) d E_i(x, \boldsymbol{\omega_i}) \] ここで、\(f_r\)をBRDFとよび、上式をBRDFに関して変形すると。 \[ f_r(x, \omega_i, \omega_o) = \frac{d L_r(x, \omega_o)}{d E_i(x, \omega_i)} = \frac{d L_r(x, \omega_o)}{L_i(x, \omega_i) |\omega_i \cdot \textbf{n}| d\omega_i} \] この式より、BRDFは(ある方向から)入射する放射照度に対する反射される放射輝度の比を表していることがわかる。そして微小放射照度\( dE_i \)は入射する放射輝度\(L_i\)を使って\(d E_i(x_i, \omega_i) = L_i(x, \omega_i) |\omega_i \cdot \textbf{n}|d\omega_i \)と表せる。なぜ、入射する放射輝度ではなく放射「照度」なのかと疑問を持つかもしれません。物体表面の微小面積に降り注ぐエネルギーは同じ輝度でも光を当てる角度によって変化する。BRDFでは、物体の特性のみで反射特性を表現したいために入射に関しては放射照度となっている。また、そのためにBRDFの単位は \([sr^{−1}]\) となる。なお、BRDFでは入射方向を実際の光の向きとは逆向きに定義する。 BRDFは名前に「反射率」とあるため取りうる値の範囲が\([0,1]\)であると思うかもしれませんが、BRDFは確率密度関数のようなもの、というか実質それそのもので、値の範囲は\([0,\infty)\)であり直接計測のできるものではありません。実際完全鏡面反射のBRDFは理論上無限大(デルタ関数)になり、「直接計測できない」のはなぜかというと、現実では計測の幅を無限小(BRDFの場合、特定の一点 + 特定の一方向 x2)にすることができないからである。似たような話はBRDFに限らず多々あり、例えば速度計による瞬間速度の計測がある。速度計も瞬間速度を直接計測できるわけではなく、十分に小さい時間幅における何かしらの移動量を測定し、平均速度を瞬間速度の近似としている。 |
| CCD・CMOSイメージセンサー | CCDセンサーとCMOSセンサーは、センサーの構造及び信号の読み出し方法が異なる。 [CCD] 1.フォトダイオードで光を受光し、電荷に変換して蓄積 2.電荷を垂直伝送路に転送 3.電荷を水平伝送路に転送 4.増幅器にて電荷を電圧に変換し出力 [CMO] 1.フォトダイオードで光を受光し、電荷に変換して蓄積 2.各画素内の増幅器にて電荷を電圧に変換 3.画素ごとのスイッチのON/OFFにより電圧を垂直信号線に転送 4.各列のノイズキャンセラーにてノイズを消去 5.列ごとのスイッチのON/OFFにより電圧を水平信号線に転送し出力 |
| 画像の再標本化 | ディジタル画像に幾何学的変換を施すと、元の画像の画素位置は、一般に変換後の標本化位置からずれる。そこで、再標本化によって返還後の画像を再び縦横等間隔に標本化された位置の値の集まりとして表現する。具体的には、 ①返還後の出力画像におけるある画素位置に対し、適用する幾何学的変換の逆変換を行い、元の入力画像で対応する位置を求める。逆変換は変換が行列で表現されている場合には、その逆行列を求めて適用する。 ②上で求めた入力画像上での位置は、一般に入力画像の画素位置からずれている。そこで、その位置の値を「何かしらの補間手法」により、周囲の画素位置の値を利用して求める。 ③上の処理を、出力画像上のすべての画素位置に対して行う。 |
| ニアレストネイバー法 | 画像の再標本化における補間手法の1つ。 値を求めたい位置を\((x,y)\)とすると、その位置の画素値\(I(x,y)\)は以下のようになる。 \( I(x,y)=f([x+0.5],[y+0.5])\) ただし、\(f(i,j)\)は入力画像の位置\((i,j)\)の画素値を、記号[]はガウス記号で、[]内の値を超えない最大の整数値を返すものである。 ニアレストネイバーは、処理が非常に単純で高速であるが、滑らかなエッジがギザギザになって現れるジャギーが発生しやすい。 |
| エンボス処理 | 入力画像\(f_1\)の濃淡を反転した画像を生成し、さらにその画像を適当な方向に数画素平行移動した画像を\(f_2\)とする。そして、以下の画像間演算を行った出力画像\(g\)がエンボス処理後の画像となる。 \(g=f_1 + f_2 -128 \) ここで、画素値は0~255の値をもつものとし、\(g\)の計算結果が0より小さいときは0、255より大きいときは255とする。エンボス処理によって、浮き彫りのような画像が得られる。 |
| オープニング処理 | 白画素を背景、黒画素を対象物としたとき、黒画素を同じ回数だけ収縮したのち膨張することで、背景中の小さい黒画素が除去される。これをオープニング処理という。 |
| クロージング処理 | 白画素を背景、黒画素を対象物としたとき、黒画素を同じ回数だけ膨張したのち収縮することで、対象物中の小さい白画素が除去される。これをクロージング処理という。 |
| ハフ変換 | 直線の検出方法。 \(xy\)画像空間中の直線は、\(\hat{a}\)を傾き、\(\hat{b}\)を\(y\)切片としたとき、以下で表すことができる。 \(y=\hat{a}x+\hat{b}\) つまり、傾きと\(y\)切片との2つのパラメータで直線を表現することができるため、これらのパラメータ空間では、\(xy\)画像空間中のある直線を1点で表すことができる。一方、\(xy\)画像空間中の直線\(l\)上の点\(x_i, y_i\)は以下によって\(ab\)パラメータ空間に写像される。 \(b=-x_ia+y_i\) すなわち、\(xy\)画像空間中の点は、\(ab\)パラメータ空間では傾き\(-x_i\)と\(b\)切片\(y_i\)の直線で表すことができる。直線\(l\)上の複数の点を\(ab\)パラメータ空間に写像すると、点の数だけ直線を描くことができ、これらの直線は\(ab\)パラメータ空間内の1点\((\hat{a},\hat{b})\)で交差する。この交差する点の座標を検出すれば、\(xy\)画像空間中の直線を決定することができる。 しかし、\(a,b\)のとりうる範囲が\(-\infty\)から\(+\infty\)となるため、\(ab\)パラメータ空間が広大になりすぎる。これを回避するために実用的には、\(xy\)画像空間中の直線を以下で表現することによって、パラメータ空間の大きさを制限する。 \(\hat{\rho}=x\cos \hat{\theta} + y\sin \hat{\theta} \) ただし、\(\hat{\rho}\)は原点から直線までの符号付き距離、\(\hat{\theta}\)は原点から直線への垂角\((0\leqq \hat{\theta} < \pi)\)である。 |
| エピポーラ線 | ステレオマッチングにおいて、カメラ1と注目している点を結ぶ直線は、カメラ2に直線として投影され、この直線をエピポーラ線とよぶ。 |
| 視差 | 平行ステレオにおいて、ステレオカメラの両光学中心を結ぶ線分のことを基線とよび、2つの画像上における投影点の横方向のずれ量は視差とよばれる。 |
| ランバートのモデル | 拡散反射表面を理想的に扱った反射モデルである。ランバート反射表面の輝度は、どの角度から見ても一定である。 \(L_{Lambert}=K_{d}\cos\theta_{i}\) \(K_{d}\)は拡散反射率、\(\theta\)は法線と光源方向のなす角。よって、視線方向には依存しない。 |
| フォンのモデル | 鏡面反射の経験的なモデル。正反射方向から見たときに最も明るく見える。 \(L_{Phong}=K_{s}(\cos\alpha)^n\) \(K_{s}\)は鏡面反射率、\(\alpha\)は正反射方向と視線方向のなす角度。\(n\)は表面の粗さを表す指標である。 フォンのモデルに従う物体表面は、\(\alpha=0\)のとき、つまり正反射方向から見たときに最も明るく見える。また、\(n\)が大きいほど理想的な鏡に近い鋭い反射となり、\(n\)が小さいほど拡散反射のような鈍い反射に近づく。 |
| ランバート面 | ランバート面の輝度は照度に比例します。点光源の方向はそのままで距離だけが変化するとき、照度の逆2乗則および照度の入射角余弦則より、点光源からランバート面に入射する光の照度は、距離の逆2乗に比例します。 |
| グラフカット | この手法は画像処理の多くの問題はエネルギー最小化問題として定式化されるので、この問題を最小カット算出に帰着する。二値画像のノイズ除去、ステレオ、及びセグメンテーション等に用いられる。画像における画素とその隣接関係 (縦横の 4 方向か斜めも含めた 8 方向) を、それぞれ頂点と双方向の有向辺に対応させて構成される有向グラフを考える。さらにその有向グラフにソースとシンクを付加して得られるフローネットワークにおける最小カットを算出する。 |
| RAM | 「RAM(ラム)」とは、英語の「Random Access Memory」(ランダム・アクセス・メモリ)の略語で、CPUが何かの処理を行うときに使われる作業用のメモリのこと。 RAMに展開されたデータは、デバイスの電源が切れるたびに消去される。 |
| ROM | ROMは英語の「Read Only Memory」(リード・オンリー・メモリ)の略語で、読み出し専用で書き込みができないメモリで、CDやゲームソフトなどがROMの代表例。 |
| インターレース走査 | 画像伝送において、データ量(動画の場合は伝送レートまたは帯域幅)を増やさずに描画回数を増やす技術である。日本語では飛び越し走査という。 ラスタースキャン方式において、画像全体を飛び飛びに走査・処理する。 よく知られたものはテレビ・ビデオ信号に使われているもので、奇数番目の走査線を先に送り、残りの偶数番目の走査線をその後に送る。これにより、フィールド周波数を倍にすることができる。たとえばNTSCでは30Hzが60Hzに、PALでは25Hzが50Hzになる。 |
| プログレッシブ走査 | インターレース走査とは異なり、すべての走査線を一本ずつ順番に伝送する方式。 |
| SIFT | SIFT(スケール不変特徴変換)はScale-InvariantFeature Transformの略で、2004年にブリティッシュコロンビア大学のD.Loweによって最初に発表された。SIFTは、画像のスケールと回転に対して不変である。 |
| 合成変換 | 右側の変換行列から処理する。 |
| バイキュービック補間 | 画像の再標本化における補間手法の1つ。 注目画素の周りの16点を参照する。バイリニア補間は周りの4点なので、バイリニア補間の方が処理が早い。 |
| 色補正 | カメラで撮影されたカラー画像のRGB値は、カメラへの入射光の分光強度分布(スペクトル)とカメラの分光感度特性により決定される。一般に、カメラの分光感度特性はデバイスに依存する。また、入射光のスペクトルは光源に依存する。したがって、同じ対象を撮影した場合においても、カメラや光源が異なれば、記録されるRGB値、すなわち画像の色は異なって見える。これらの、カメラや光源に依存する画像の色を補正して、人間の色知覚に基づくCIE-XYZ表色系や、sRGB色空間での色を表現する処理を色補正と呼ぶ。 |
| 4バイラテラルフィルタ | エッジ保存平滑化フィルタの一種。ガウシアンフィルタがベースのフィルタで、ガウシアンフィルタでは画面全体を一様にぼかしていましたが、バイラテラルフィルタでは画像のエッジとなる部分を残しながらぼかしていく。 具体的には、中心の輝度値との違いで重み付けしてエッジとなっている部分を保持する。 処理前画像を\(f(i,j)\)、処理後画像\(g(i,j)\)をとすると。 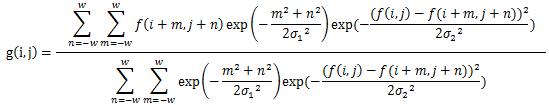 |
| 標準分光視感効率 | 可視光線(人間の目が感じることのできる光)は電磁波の一部で、波長は380nm(ナノメートル)~780nmまでだが、波長によって感じ方が異なり、明るい所では555nmの場合に感度が最大になる。 |
| HSI色空間 | 色相 (Hue)、彩度 (Saturation)、輝度(Lightness / Luminance または Intensity)の3つの成分からなる色空間。 HSL、HSIと呼ばれることもある。HSV色空間によく似ている。 ・色相: 色味を0から360度の範囲の角度で表す。0度は赤で、その反対側に位置する180度は赤の反対色にあたる青緑。すなわち、反対色を見つけるのも容易。色相についてはHSVと同じ。 ・彩度: HSVとは違い、純色から彩度が落ちるということは、すなわち灰色になっていくという考え方に基づいている。 ・輝度: 明度100%を純色としてそこからどれだけ明るさが失われるかで表すHSVとは違い、輝度0 %を黒、100 %を白とし、その中間 (50 %) を純色とする。50 %以下はHSVの明度を示し、50 %以上はHSVの彩度を示すと考えると分かりやすい。 |
| HSI6角錐モデル | 赤の反対側はシアン。上面の辺は彩度最大。 HSI円柱モデルの場合は上面は白となる。 |
| 色相環 | 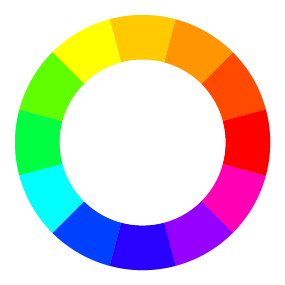 赤から、オレンジ、黄、緑、青を経て、紫 赤から、オレンジ、黄、緑、青を経て、紫 |
| 色と波長 | 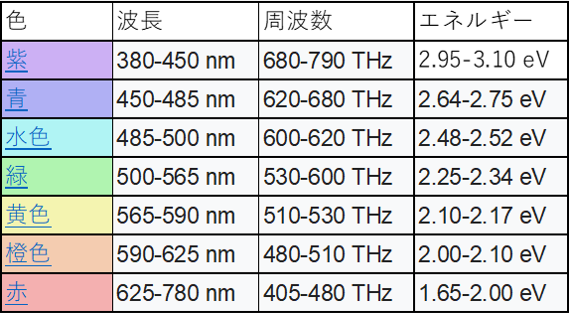 |
| 2次元カボールフィルタ | 画像処理のテクスチャー解析等に用いられる線型フィルタの一種。(2次元のガボールフィルタでは)画像の各点周りの局所領域において、方向毎に特定の周波数成分を抽出することができる。 細部が異なる種々の定義があるが、基本的にはガウス関数(ガウシアンエンベロープとも呼ばれる)と三角関数(搬送波とも呼ばれる)の積として定義される。  (cv2.getGaborKernelにて作成) \( g(x,y,\lambda,\phi)=\exp(-\frac{x^2+y^2}{2\sigma^2})\cos\{2\pi\lambda(x\cos\phi+y\sin\phi)\} \) \(\lambda:\)フィルタパターンの周波数 \(\phi:\)フィルタパターンの向き \(\sigma:\)フィルタの広がり |
| 点拡がり関数 | ボケやぶれにより劣化した画像は、原画像に空間フィルタリング処理を施した画像であると考えられる。よって、劣化した画像g(x,y)は原画像f(x,y)およびフィルタ関数h(x,y)を用いて以下の畳み込み積分により表される。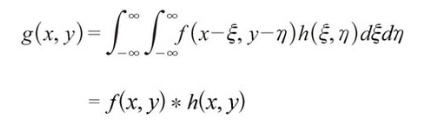 劣化を表すフィルタ関数h(x,y)は点拡がり関数とも呼ばれる。 2次元デルタ関数は、全く劣化の無いフィルタで、以下のように定義される。 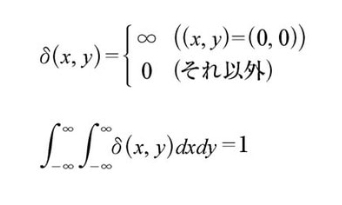 |
| ウィーナフィルタ | 画像内の加法性ランダムノイズを削減することを目的に開発された最初の手法の 1 つ。このフィルタは加法性ノイズがピクセル位置から独立した定常ランダムプロセスであるという前提に基づいており、そのアルゴリズムは、元の画像と再構築された画像との間の二乗誤差を最小化する。 フィルタ後の画像内のピクセル yは、次の変換式によって、ノイズを含む入力画像のピクセル x から計算される。 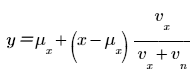 ここで、μx と vx はピクセル x の近傍における平均と分散であり (近傍の大きさはこの関数への引数 win_h と win_w によって決まる)、vn は入力画像から推定された加法性ノイズの分散である。出力の各ピクセルは、入力ピクセルの近傍からの局所平均値と局所コントラスト項 (x – μx) の和である。局所コントラスト項は、ノイズの分散 (vn) が画像の分散 (vx) よりもかなり小さい、ディテールが多い領域では、スケール係数がほぼ 1 になり、フィルタをほとんど行わない状態で出力ピクセル y が入力ピクセル x に非常に近くなり、ディテールが少ない領域では、画像の分散が小さく、出力ピクセルが局所平均に近づく (ローパスフィルタが適用された状態になる) ように尺度化される。 |
| プレノプティック関数 ライトフィールド | 光が通る3次元位置\((X,Y,Z)\)、光線の方向\( (\theta,\phi) \)、光線の波長\(\lambda\)、時刻\(t\)を用いて、光線の情報を\(l(X,Y,Z,\theta,\phi,\lambda,t)\)として記述したものをプレノプティック関数と呼ぶ。 このような光線で埋められた3次元空間をライトフィールドと呼ぶ。 |
| オイラー数 | オイラー数=(連結成分の数)ー(穴の数) |
| チャンファーマッチング | チャンファーマッチングとはエッジ情報を用いてパターン探索を行う方法。 ①エッジ検出法で入力画像、テンプレート画像のエッジ画像を作成 ②入力画像(エッジ画像)の距離変換画像を作成(エッジからの距離を示した画像) ③作成した距離画像とテンプレート画像(エッジ画像)の相違度を求める ④最も相違度が小さくなった場所をパターンの位置として特定する ちなみに相違度は (相違度) = (テンプレートのエッジ画像の画素)*(入力した距離変換画像の画素値)の総和 |
| SAD(テンプレートマッチング) | SAD(Sum of Absolute Difference)では、「画素値の差分の絶対値の和」で類似度を評価します。 この場合も値が最小になる場所が類似度が最も高いことになります。 入力画像の画素値を また、テンプレート画像の幅を 走査位置が SADとSSDを比較すると、 ・SADの方が計算量が少なく、外れ値の影響を受けにくい ・SSDの方が、コントラストの影響をいくらか受けにくい |
| SSD(テンプレートマッチング) | SSD(Sum of Squared Difference)では、「画素値の差分の二乗和(二乗誤差)」で類似度を評価します。 この場合、値が最小になる場所が類似度が最も高いことになります。 入力画像の画素値を また、テンプレート画像の幅を 走査位置が |
| DoG | Difference of Gaussian 特徴点とその領域の大きさを表すスケールを検出する方法。複数のDoG画像を用いて計算することができる。DoGはLoG(Laplacian of Gaussian)を近似したものであり、σの値を大きくしながら複数のσでガウス関数G(σ)と入力画像Iを畳み込んだ平滑化画像Lを計算し、σが隣同士の平滑化画像Lの差分により、DoG画像D(σ)を求める。このとき、注目画素のD(σ)の値が最大となるσがその特徴点のスケールとなる。 |
| ウェーブレット変換 | p.405 |
| トランス・スパロウのモデル | 鏡面反射 |
| オーレン・ネイヤーのモデル | 拡散反射 |
| 光ショットノイズ 暗時ノイズ | 受光素子から読み出す電圧値は受光素子に到達した光子数に比例するため、出力電圧には光子数に比例する揺らぎが含まれる。この揺らぎの標準偏差を光ショットノイズと呼ぶ。撮影対象が明るいほど、受光素子に到達する光子数は多くなるため、光ショットノイズは大きくなる。 受光素子の出力電圧には、光ショットノイズの他に、暗電流ノイズ、読み出しノイズ、固定パターンノイズなどがある。これらのノイズは受光素子に到達した光子数即ち露光量には無関係で、暗時ノイズと呼び、まとめて平均0のガウスノイズで近似できる。 |
| アフィン変換、射影変換 | アフィン変換:未知パラメータ6個→3組の点が必要。 \(\left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = \left( \begin{matrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{matrix} \right) \left( \begin{matrix} x \\ y \\ 1 \end{matrix} \right)\) 射影変換:未知パラメータ8個→4組の点が必要。 \(\left( \begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right) = \left( \begin{matrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & 1 \end{matrix} \right) \left( \begin{matrix} x \\ y \\ 1 \end{matrix} \right)\) |
| 符号化開口 | 入射した光の位置を符号化。非合焦時のボケ除去に有効。 |
| 符号化露光 | 入射した光の通過時刻を符号化。同物体のブレ除去に有効。 |
| 畳み込み積分 | \(f_1(x,y)\ast f_2(x,y)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f_1(\xi,\eta) f_2(x-\xi,y-\eta)d\xi d\eta\) |
| 畳み込み積分 のフーリエ変換 | \(F{\space}\)を\({\space}\)内の関数のフーリエ変換を表すとすると、 \(F\{f_1(x,y)\ast f_2(x,y)\}=F\{f_1(x,y)\}F\{f_2(x,y)\}\) が成り立つ。 つまり、2つの関数の畳み込み積分の結果をフーリエ変換したものは、それぞれの関数のフーリエ変換の積に等しくなる。 |
| フーリエスペクトル(振幅スペクトル) | 画像\(f(s,y)\)のフーリエ変換\(F(u,v)\)は一般に、実部と虚部を有する複素数となる。フーリエスペクトルは\(F(u,v)\)の絶対値に対応する。 ・画像のエッジと直交する方向にフーリエスペクトルは伸びる。強いエッジはフーリエスペクトルでも大きな値となる。 ・低周波数成分のみだとフーリエスペクトルは中央に集まる。 |
| ミーンシフトトラッキング | 準備として最初のフレーム画像において対象物体を囲む領域を指定し、色ヒストグラムを算出しておきます。以降のフレームでは、直前のフレームで対象物体が存在した位置周辺の領域で色ヒストグラムを算出し、記憶している色ヒストグラムとのバタチャリヤ係数を評価します。バタチャリヤ係数は微分可能であるため、バタチャリヤ係数の極大点に向かう勾配方向を求めることによって効率よく探索します。初期の探索スタート位置を中心とする領域が現在の物体位置を中心とする領域と重なっている画素の重みを大きくし、そうでない画素の重みを小さくします。それらの重みで加重平均して、つぎの探索位置を求めると現在の物体位置に近づくというしくみです。 |
| KLT(Kanade-Lucas-Tomasi)トラッカー | コーナー点を特徴点として検出しオプティカルフローを計算する。 Tにおける特徴点の画素位置からIにおける特徴点の画素位置へ向かうオプティカルフローfを求めることが目的です。しかし、一度の計算ではオプティカルフローfを精度よく求めることができない可能性があるため、繰り返し計算を行います。fによって変形(ワープ)したI(f)がTに一致すれば、そのfが解ですが、一度の計算で求めたfではI(f)とTが一致しないことがあります。そこで、Tにおける特徴点の画素位置からI(f)における特徴点の画素位置へ向かうオプティカルフローΔfを求めます。これにより、f+Δfはfと比較して正解に近づきます。これを繰り返すことで精度よくオプティカルフローを求めることができます。 |
| イメージピラミッドを用いたオプティカルフロー | オプティカルフローを求める方法。 イメージピラミッドは、原画像を例えば縦横1/2にした縮小画像を生成し、再度その縮小画像を1/2に縮小することを繰り返してつくられます。まず、最も小さな縮小画像においてオプティカルフローを求めることで大きな動きを把握します。次に、そのオプティカルフローを2倍して、画像解像度を1段階あげた画像に配置します。その画像では、配置されたオプティカルフローの先端からの微小な変異(差分フロー)を求めます。それら2つのフローを合成(ベクトルを加算)します。これを原画像と同じ解像度まで繰り返すことで最終的なオプティカルフローが得られます。 |
| 画像座標系とカメラ座標系 | 画像座標系で線分でも、カメラ座標系(ワールド座標)では曲線や複数の線分である可能性がある。 |
| アクティブステレオ法 | 距離画像の取得方法。 ・スリット光投影:スリット光を投影してできる像の位置から、三角測量の原理によって距離を計測する。 ・パターン光投影:計測空間を光パターンでコード化することにより、少数枚の画像から密な距離画像を得る方式。投影するパターンには、カラーパターン、濃度傾斜変調パターン、擬似ランダムコード化パターン、多重コード化パターン、チェッカーボードパターン、リングパターンなどがある。 |
| カメラキャリブレーション | 既知のワールド座標と画像座標の最低6組の対応を使って、透視投影行列を求めること。 |
| カメラレンズの絞り値 | 写真の明るさ\( \propto \frac{1}{f^2} \quad f:\)絞り値 ・絞りが大きいほど写真は暗くなる。 ・絞りが小さいほど色々な光が入るので明るいが、ボケやすい。 |
| 被写界深度 | 写真撮影でピントを合わせた部分の前後のピントが合っているように見える範囲。 被写界深度を深めるには、レンズ焦点距離を短く、レンズ絞り値を大きくする。 |
| 鮮鋭化フィルタ |  |
| ノンローカルミーンフィルタ | エッジを残しながら、平滑化を行うエッジ保存平滑化フィルタの一つである。注目画素を中心とするテンプレートと参照画素を中心とするテンプレートの類似度(L2距離)から重みを計算する。テンプレートの類似度が高いほど重みは大きくなる。 |
| ケニーのエッジ検出 | ノイズの低減と微分、勾配の大きさが最大となる位置の検出、しきい値処理の3段階の処理によりエッジを検出します。 ・ノイズ低減のためのガウシアンフィルタの標準偏差\(\sigma\)を大きくすると、画像の大まかな特徴を表すエッジだけが検出されるようになります。 ・上側しきい値\(Th_{high}\)により、隣接画素がエッジであるかどうかによらずに検出されるエッジの数を調整できます。 ・下側しきい値\(Th_{high}\)により、勾配の大きさが小さいエッジをどこまで残すのかを調整できます。 |
| LoGフィルタ | ガウス分布のラプラシアン(2階偏微分) \(\triangledown^2h_{g}(x,y)=\frac{x^2+y^2-2\sigma^2}{2\pi\sigma^6}\exp{(-\frac{x^2+y^2}{2\sigma^2})}\) ガウシアンフィルタによる平滑化とラプラシアンフィルタによるエッジ抽出の合成フィルタ。σの値を大きくすると、強い平滑化が行われるため、細かなエッジは無くなり、大まかなエッジが残る。 |
| モード法 | ヒストグラムの山と山の間の谷の底をしきい値として2値化する。 |
| p-タイル法 | 黒or白の画素数が予測できるとき、画素数に応じてしきい値を決定する。 |
| 判別分析法 | 大津の2値化。 クラス内分散が最小、クラス間分散が最大となるようにしきい値を決定する。 |
| インバースライティング | シーン中の物体の陰影をもとに光源分布を推定する方法。光が重ね合わせの原理を満たすことを利用している。 |
| DPCM | Differential Pulse Code Modulation 予測符号化の代表的な方法。画素値をそのまま伝送するのではなく、伝送しようとする画素値とその画素値の予測値との差分を伝送する方式です。 |
| 錐体細胞 | 錐体細胞は含まれる視物質(オプシン)の違いにより、反応する光の波長分布に差がある。Lはlongの略で3つの錐体のなかで最も長波長(赤色)によく反応する。またMはmiddle、Sはshortの略でこの順に反応する波長の分布が短波長側にズレる。人の脳はL,M,Sの各錐体の反応の比率によって色を知覚していると考えられている。 |
| 杆体細胞 | 光の強弱に応じた明暗を認識し、表面的には色覚にはほぼ関与しないが、感度が高い。暗所では錐体細胞はほとんど働かず、主に桿体細胞が働く。このため暗所では、色の識別が困難となる。特に赤色の長波長が見えにくい。 |
| プルキニエ現象 | 色は網膜の視細胞で感知しているが、明るい場所では赤が鮮やかに遠くまで見え、青は黒ずんで見える。一方、暗い場所では青が鮮やかに遠くまで見えるのに対して、赤は黒ずんで見える。これは、杆体と呼ばれる視細胞の働きによるもので、人の目は暗くなるほど青い色に敏感になる。 |
| SIFT特徴量 | 特徴点の検出時にスケールも検出することで、拡大・縮小に不変、オリエンテーションを算出することで回転にも不変な特徴量である。 勾配強度と勾配方向から作成した重み付き勾配方向のヒストグラムのピークにおける方向に座標軸を合わせて特徴量を記述するため、回転に不変な特徴量となる。 |
| JPEG方式 | RGBカラー画像をYCbCr色空間に変換することで、現画像を輝度成分Y、色差成分Cb,Crの3成分に分解する。さらに、2つの色差成分だけを間引いて情報量を削減する。その後、画像を8×8画素のブロックに分割してから2次元DCTを施し、情報量の多い低周波数成分と情報量の少ない高周波数成分に分けて、あまり情報の含まれない高周波数成分を効率よく圧縮できるようにし、最後に、ハフマン符号化を行い圧縮する。 (カラー画像を輝度成分と色差成分に変換すると、色差成分は0を中心とする比較的狭い範囲に集中して、色差成分値の出現確率に偏りが生じるため、符号化の際に平均符号長を短くできる。) |
| マンセルの色立体 | 色相・明度・彩度の3要素を立体的・感覚的に表したものである。中心軸は明度を表しており、下が0(黒)で上が10(白)。外側に行くほど彩度が高くなり、水平断面では円周位置で色相を表している。 |
| CIE-L・a・b色空間 | p.75 2色間の色差Δはユークリッド距離として求められる。 |
| CIE–XYZ表色系 | p.73 |
| エッジセンシング補間 | 上下方向と左右方向の画素値の変化を比較し、変化が滑らかな方向の画素値のみを用いて補間する。 |
| マハラノビス距離 | \(D_{M}(x)=\frac{\sqrt{(x-\mu)^2}}{\sigma} \) |
| kd-tree法 | k次元のユークリッド空間にある点を分類する空間分割データ構造である。 ・木構造を下降すると共に、分割平面を選択する軸を巡回するようにする。例えば、根においてx軸に垂直な平面とし、根の子ではy軸に垂直な平面とし、根の孫ではz軸に垂直な平面とする、というように軸を巡回するように選択していく。 ・各ステップで、分割平面生成で選択される点は、kd木に入れる全ての点の対応する軸の座標値の中央値となる点とする。なお、前提として全ての点の集合がアルゴリズムの先頭で得られるものとする。 |
| 放射量 | 単位時間あたりの光源の放射エネルギーは放射束[W]と呼ばれる。光源から放たれた光がある面を照射するとき、照射面の単位面積に対して単位時間に照射される放射エネルギーは放射照度[W/m2]と呼ばれる。一方、観測方向から免状の放射源を見たとき、見る方向に投影した単位面積あたりの放射強度は放射輝度[W/sr・m2]と呼ばれる。 |
| 反射成分の分離について | ・色に基づく反射成分の分離では、拡散反射成分と鏡面反射成分の色の違いを利用する。 ・2色性反射モデルによると、拡散反射成分の色は、光源の色と物体の分光反射率の両方に依存する。 ・2色性反射モデルによると、鏡面反射成分の色は光源の色と一致する。 ・拡散反射成分の偏光状態は、入射光によらず非偏光である。 |
| 透視投影行列 カメラキャリブレーション | ワールド座標の同次座標から画像座標の同次座標への変換は、3行4列の透視投影行列を用いて表すことができる。あらかじめ位置が分かっている空間中の点および、その画像上への投影点を用いて透視投影行列を求めるカメラキャリブレーションについて考える。透視投影行列は定数倍しても同じ投影を表すため、適当な成分を1に固定すると、未知数の数は11個になる。空間中の位置とその投影点の画像上の位置が1組与えられると、透視投影行列に関する方程式が2個得られる。したがって、既知の位置座標の組が最小で6組あれば、透視投影行列を求めることができる。 |
| 2次元DCT(JPEG)のノイズ | モスキートノイズ: オブジェクト境界のもやもやしたパターン(蚊の大群がいるように見えるから) ブロックノイズ: ブロック境界の不連続性 |
| 単語 | 内容 |
| 職務著作 | 職務の一環で文芸・音楽・映像・ソフトウェアといった著作物を創作した場合、創作した個人本人ではなく、創作を指揮・監督した雇用主や業務委託者が著作権を有するとする著作権法上の概念。 |
| 特許権 実用新案権 意匠権 商標権 | 出願日から20年 出願日から10年 出願日から25年 登録日から10年(以降、10年ごとに更新可能) |
| 公衆送信権 | 他人の著作物をネットにアップする場合抵触する |
| 産業財産権 | ・特許権 ・実用新案権 ・意匠権 ・商標権 |
| 著作権におけるデータベース | データベースでその情報の選択または体系的な構成によって創造性を有するものは著作物となる。一方で、思想や感情を包含しないデータそのものは保護されない。 |
| 映画、無名、団体名義の著作権 | 公表後70年間 |
| アニメ、ゲームソフト | 映画の著作権となる |
| 学術的な図面、図表 | 著作物となる |

コメント