部分的最小二乗回帰で次元削減(partial least squares regression, PLS回帰)

この記事では、sklearnでの部分的最小二乗回帰の使い方を紹介します。備忘録として作成します。

PLS回帰とは？
実際の処理
まとめ

PLS回帰とは？

線形の回帰分析手法の１つであり、説明変数の次元削減に利用できます。教師データとの共分散が最大となるように抽出した主成分を利用して回帰を行います。

次元削減では主成分分析(PCA)がよく用いられますが、教師データがある状況では部分的最小二乗回帰が有効です。詳しいアルゴリズムについては、wikipediaやこちらのページが詳しいです。

ここでは、主成分分析の結果と比較しながらPLS回帰による次元削減の手順を例示します。

実際の処理

ライブラリのインポート

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.cross_decomposition import PLSRegression
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split

データセットを読み込みます。ここではカリフォルニアの住宅価格のデータセットを使用します。

# データセット読み込み
dataset = fetch_california_housing(as_frame=True)
X = dataset.data
y = dataset.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

PLS回帰とPCAを適用します。どちらも抽出する主成分数は2個にしています。

# PLS1
pls1 = PLSRegression(n_components=2)
pls1.fit(X_train, y_train)
X_train_pls = pls1.transform(X_train)
X_test_pls = pls1.transform(X_test)

# PCA
pca = PCA(n_components=2)
pca.fit(X_train, y_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)

テストデータについて、PLS回帰とPCAで抽出した主成分と、目的変数のプロットを作成します。

# 次元削減後のプロット
plt.figure(figsize=(12, 10))
plt.subplot(221)
plt.scatter(X_train_pls[:, 0], y_train, label="train", marker="o", s=2)
plt.scatter(X_test_pls[:, 0], y_test, label="test", marker="o", s=2)
plt.xlabel("x scores")
plt.ylabel("y")
plt.title(
    "PLS1: X_comp1 vs Y (test corr = %.2f)"
    % np.corrcoef(X_test_pls[:, 0], y_test)[0, 1]
)

plt.legend(loc="best")


plt.subplot(222)
plt.scatter(X_train_pls[:, 1], y_train, label="train", marker="o", s=2)
plt.scatter(X_test_pls[:, 1], y_test, label="test", marker="o", s=2)
plt.xlabel("x scores")
plt.ylabel("y")
plt.title(
    "PLS1: X_comp2 vs Y (test corr = %.2f)"
    % np.corrcoef(X_test_pls[:, 1], y_test)[0, 1]
)

plt.legend(loc="best")


plt.subplot(223)
plt.scatter(X_train_pca[:, 0], y_train, label="train", marker="o", s=2)
plt.scatter(X_test_pca[:, 0], y_test, label="test", marker="o", s=2)
plt.xlabel("x scores")
plt.ylabel("y")
plt.title(
    "PCA: X_comp1 vs Y (test corr = %.2f)"
    % np.corrcoef(X_test_pca[:, 0], y_test)[0, 1]
)

plt.legend(loc="best")


plt.subplot(224)
plt.scatter(X_train_pca[:, 1], y_train, label="train", marker="o", s=2)
plt.scatter(X_test_pca[:, 1], y_test, label="test", marker="o", s=2)
plt.xlabel("x scores")
plt.ylabel("y")
plt.title(
    "PCA: X_comp2 vs Y (test corr = %.2f)"
    % np.corrcoef(X_test_pca[:, 1], y_test)[0, 1]
)

plt.legend(loc="best")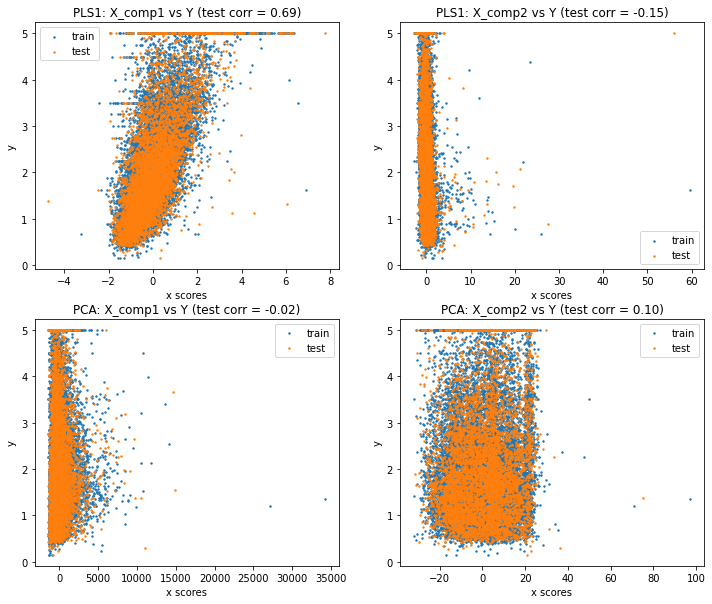

PLS回帰では、主成分１が目的変数との相関が高くなるように抽出できていることが分かります。一方でPCAの場合は目的変数との相関がほぼ見られません。これは、主成分の抽出の際に目的変数との共分散を考慮していないためです。

このように、どちらも次元削減の手法として利用できるPLS回帰とPCAですが、回帰分析を目的としている場合は、PLS回帰を利用することが好ましいです。

最後に、PLS回帰の主成分１の相関係数を見ると、0.69となっています。元データの目的変数と説明変数の相関係数を確認すると、8個の説明変数のうち「MedInc(所得の中央値)」が0.676で最も高いようです。よって、PLS回帰によって元データよりも相関係数が高い主成分を抽出することができています。

corr = pd.concat([y_test, X_test], axis=1).corr()
corr['MedHouseVal']

MedHouseVal    1.000000
MedInc         0.676196
HouseAge       0.109738
AveRooms       0.140798
AveBedrms     -0.033096
Population    -0.020910
AveOccup      -0.020817
Latitude      -0.144643
Longitude     -0.046410
Name: MedHouseVal, dtype: float64